The metafactor C++ library was primarily developed for compile-time factorization of integers up to 32-bit unsigned maximum. As a side-effect, using the algorithms of this library, I could generate big list of primes at compile-time. It turns out that a list of primes less than 65536 (16-bit unsigned integers) can be generated by Clang 3.8 C++ compiler within 5 minutes of compilation time. Apparently, such a list is enough to check any 32-bit unsigned integer for primality or can be used for other purposes.

The procedure of the primes generation is simple: I use formulas 6k+r, 30k+r, 210k+r, etc. to obtain a prime candidate, which than should still be checked for primality either by the currently growing list of primes or by one of the same formulas. The formulas represent a subset of natural numbers containing all the prime numbers. To know how k and r are defined read this former article. A natural idea is to use those formulas consequently reducing the subset and so accelerating the generation process. But in fact, the set of reminders r is growing so fast, that the usage of formulas other than three above has no benefit. I implemented and tested this hierarchic idea and left it under Hierarchic namespace in the source code, but would not suggest to use it.

The algorithm

To achieve the goal of a primes list generation up to 65536, I tried different strategies and tested them with GCC 5.4 and Clang 3.8 under Ubuntu Linux 16.04, met some compiler limitations, but finally found compromises and listed the best three of them in metaprimes.cpp. They can be selected with MODE=1,2 or 3 compiler option. The end of the primes list should be defined with LIMIT compiler option (e.g. LIMIT=1000 will generate a list of primes less than 1000).

The most efficient way to generate the list of primes at compile-time I found, is a single recursion using one of the formulas 6k+r, 30k+r, 210k+r to get a prime candidate, while each prime candidate is then tested for primality using again the formulas 6k+r or 30k+r up to the factor, which square is not greater than the prime candidate. Note, that the list of primes for the primality check is not available in this single recursion. To reduce the overall recursion deepness, I separated the recursion over k from the recursion over the reminders r. That was crucial to make the algorithm working with Clang for large LIMIT values.

Two implementations

Since the work on this heavy metaprogramming has started long before C++11 standard, I still follow two versions of the code:

1. For C++ 2003 (compiler option CPP=98). It is based on Liki library by A. Alexandrescu using Loki::Typelist for the compile-time storage of the generated primes list. Loki::Typelist is a recursive class template with a constant time insertion of a type in the beginning and all the generation algorithms profit from this property. The largest primes list (LIMIT=65536) could be generated by GCC 5.4 in ca. 1 hour of compile-time and in ca. 5,5 min (see the plots below for more details)
2. For C++11 and above (compiler option CPP=11). It is based on variadic template parameters wrapped in a typelist<…> class template for the compile-time storage of the generated primes list. A type insertion in this case is compiler-dependent. The tests have shown slower compilation times (ca. factor 2) using GCC 5.4 for this varsion comparing to the first one. Clang has nearly the same high performance, but suffers from the template depth. The only formula 210k+r could generate all the primes up to 65536 using Clang. Other cases have crashed.

The classical sieve

When I started to write this article, I realized, it will be incomplete without to compare my algorithm against the classical sieve of Eratosthenes. I implemented it within the first version using Loki::Typelist. In the first step, I generate a full list of prime candidates up to the LIMIT using the formulas 6k+r or 30k+r and then eliminate the non-primes consequently using the factors starting with 5 for the first formula and with 7 for the second obtaining the next filtered list. Then the second factor is taken from the filtered list and so on up to the factor, which square is not greater than the LIMIT.

Interesting is, that the compile-times of this different algorithm are very close to the selected one by using GCC 5.4. Clang could compile only up to 4000 primes due to deep recursion in the initial candidate list and crashed for larger lists.

Results

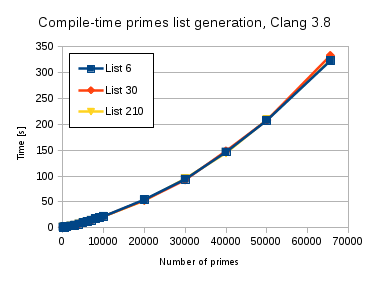
Both plots below are for the first version (using Loki::Typelist), which is the preference. It has shorter compile-times using GCC 5.4 and similar compile-times using Clang 3.8 comparing to the second version (using variadic templates). In the second version, Clang 3.8 could compile the longest primes list generation using the formula 210k+r only, otherwise it crashed, while with the first version Clang could use all the formulas to compile the longest list.

GCC 5.4 takes long compilation times and a lot of RAM and spends around 1 hour for the longest list. The deviations in compile-time for the large lists can be caused be the limits of RAM (24Gb on my workstation) and involvement of swap. Clang 3.8 is about 10 times faster than GCC 5.4, uses much less RAM, but suffers from the deep template recursion. Probably, I miss certain Clang compiler switch. Please, tell me, if you know it.